Loading required package: epiworldRThank you for using epiworldR! Please consider citing it in your work.
You can find the citation information by running
citation("epiworldR")Warning
The dataset used in this vignette is still under review. Please take these results with caution.
During the 2025 US Measles outbreak, the number of cases in the state of Utah started to climb quickly in the Short Creek region (on the Utah-Arizona border). This vignette shows how we can use the mixing model of the measles R package to do scenario modeling of the situation using both age and school data.
Set up
We start by loading the measles R package. Since the package depends on epiworldR, epiworldR is loaded automatically too:
For the data, we need two datasets: information about the population distribution by age and vaccination status, and the contact matrix. The measles R package comes with a pre-processed dataset that was created using the multigroup.vaccine R package. We can load the needed data using the data() function:
Let’s take a look at the datasets:
short_creek age_labels agepops agelims vacc_rate
1 under5 563 0 0.9300000
2 5to9 569 5 0.9300000
3 10to14s1 250 10 0.0640000
4 10to14s2 350 10 0.3685714
5 10to14s3 190 10 0.4210526
6 15to19s4 86 15 0.2325581
7 15to19s5 150 15 0.3666667
8 15to19s6 84 15 0.5952381
9 20to24s7 114 20 0.2368421
10 20to24s8 108 20 0.3703704
11 20to24s9 205 20 0.4536585
12 25to29 523 25 0.9300000
13 30to34 227 30 0.9300000
14 35to39 307 35 0.9300000
15 40to44 222 40 0.9300000
16 45to49 302 45 0.9300000
17 50to54 329 50 0.9300000
18 55to59 164 55 0.9300000
19 60to64 99 60 0.9300000
20 65to69 68 65 0.9300000
21 70+ 63 70 0.9300000
# Looking at the first 5 columns
short_creek_matrix[, 1:5] |>
round(2) under5 5to9 10to14s1 10to14s2 10to14s3
under5 0.38 0.16 0.03 0.04 0.02
5to9 0.09 0.55 0.05 0.06 0.04
10to14s1 0.02 0.07 0.58 0.10 0.05
10to14s2 0.02 0.07 0.07 0.61 0.05
10to14s3 0.02 0.07 0.07 0.10 0.56
15to19s4 0.01 0.02 0.03 0.05 0.03
15to19s5 0.01 0.02 0.03 0.05 0.03
15to19s6 0.01 0.02 0.03 0.05 0.03
20to24s7 0.04 0.03 0.02 0.02 0.01
20to24s8 0.04 0.03 0.02 0.02 0.01
20to24s9 0.04 0.03 0.02 0.02 0.01
25to29 0.08 0.07 0.02 0.03 0.01
30to34 0.12 0.11 0.03 0.04 0.02
35to39 0.10 0.12 0.04 0.06 0.03
40to44 0.06 0.10 0.06 0.08 0.04
45to49 0.06 0.06 0.04 0.06 0.03
50to54 0.05 0.07 0.04 0.05 0.03
55to59 0.07 0.07 0.03 0.04 0.02
60to64 0.09 0.08 0.03 0.04 0.02
65to69 0.08 0.09 0.03 0.05 0.03
70+ 0.07 0.08 0.04 0.05 0.03One important thing to note is that the data in short_creek must coincide with that in the contact matrix, particularly, there should be one entry in the data.frame for each row/column of the contact matrix.
Creating the model
To create the model, we do the following:
N <- sum(short_creek$agepops)
measles_model <- ModelMeaslesMixing(
n = N,
prevalence = 1 / N,
contact_rate = 15 / 0.9 / 4,
transmission_rate = 0.9,
vax_efficacy = 0.97,
contact_matrix = short_creek_matrix,
hospitalization_rate = 0.1,
hospitalization_period = 7,
days_undetected = 2,
quarantine_period = 21,
quarantine_willingness = 0.9,
isolation_willingness = 0.9,
isolation_period = 4,
prop_vaccinated = 0.95,
contact_tracing_success_rate = 0.8,
contact_tracing_days_prior = 4
)Now, since this is a mixing model, we are required to specify the entities. To do so, we can either use the functions entity() and add_entity(), or use the wrapper add_entities_from_dataframe() as follows:
# Adding the entities to the model
add_entities_from_dataframe(
model = measles_model,
entities = short_creek,
col_name = "age_labels",
col_number = "agepops",
as_proportion = FALSE
)We can also specify the vaccination rates. There are multiple ways in which we can do that. The default behavior of the model is, at each run, randomly sample prop_vaccinated percent of the population and assign the vaccine. Thus, the number of vaccinated individuals will be constant across simulations. Nonetheless, since the schools and age groups have different vaccination rates, it is better to use the distribute_tool_to_entities() function. Like the add_entities_from_dataframe() function, the distribute_tool_to_entities() function simplifies the process:
# Creating the distribution function
dist_fun <- distribute_tool_to_entities(
prevalence = short_creek$vacc_rate,
as_proportion = TRUE
)
# Setting the distribution function
measles_model |>
get_tool(0) |>
set_distribution_tool(dist_fun)Now, we can specify what to record from the simulation.
measles_model |>
run_multiple(
ndays = 100,
nsims = 100,
seed = 8812,
saver = make_saver("outbreak_size", "hospitalizations"),
nthreads = 2L
)Starting multiple runs (100) using 2 thread(s)
_________________________________________________________________________
_________________________________________________________________________
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| done.After calling the function run_multiple(), the C++ function will write the information to disk. Before we read in the data, we can take a look at the summary of the model, which will give us an overview of the last run, including how much time it spend per simulation, and what is the transsition matrix for the current run.
summary(measles_model)________________________________________________________________________________
________________________________________________________________________________
SIMULATION STUDY
Name of the model : Measles with Mixing and Quarantine
Population size : 4973
Agents' data : (none)
Number of entities : 21
Days (duration) : 100 (of 100)
Number of viruses : 1
Last run elapsed t : 0.00s
Total elapsed t : 6.00s (100 runs)
Last run speed : 29.61 million agents x day / second
Average run speed : 8.21 million agents x day / second
Rewiring : off
Global events:
- Update infected individuals (runs daily)
Virus(es):
- Measles
Tool(s):
- Vaccine
Model parameters:
- (IGNORED) Vax improved recovery : 0.5000
- Contact rate : 4.1667
- Contact tracing days prior : 4.0000
- Contact tracing success rate : 0.8000
- Days undetected : 2.0000
- Hospitalization period : 7.0000
- Hospitalization rate : 0.1000
- Incubation period : 12.0000
- Isolation period : 4.0000
- Isolation willingness : 0.9000
- Prodromal period : 4.0000
- Quarantine period : 21.0000
- Quarantine willingness : 0.9000
- Rash period : 3.0000
- Transmission rate : 0.9000
- Vaccination rate : 0.9500
- Vax efficacy : 0.9700
Distribution of the population at time 100:
- ( 0) Susceptible : 4972 -> 4969
- ( 1) Exposed : 1 -> 0
- ( 2) Prodromal : 0 -> 0
- ( 3) Rash : 0 -> 0
- ( 4) Isolated : 0 -> 0
- ( 5) Isolated Recovered : 0 -> 0
- ( 6) Detected Hospitalized : 0 -> 0
- ( 7) Quarantined Exposed : 0 -> 0
- ( 8) Quarantined Susceptible : 0 -> 0
- ( 9) Quarantined Prodromal : 0 -> 0
- (10) Quarantined Recovered : 0 -> 0
- (11) Hospitalized : 0 -> 0
- (12) Recovered : 0 -> 4
Transition Probabilities:
- Susceptible 1.00 0.00 - - - - - - - - - - -
- Exposed - 0.93 0.06 - - - - 0.01 - - - - -
- Prodromal - - 0.20 0.80 - - - - - - - - -
- Rash - - - 0.20 0.20 - - - - - - - 0.60
- Isolated - - - - 0.50 - - - - - - 0.50 -
- Isolated Recovered - - - - - - - - - - - - -
- Detected Hospitalized - - - - - - - - - - - - -
- Quarantined Exposed - 0.05 - - - - - 0.95 - - - - -
- Quarantined Susceptible - - - - - - - - - - - - -
- Quarantined Prodromal - - - - - - - - - - - - -
- Quarantined Recovered - - - - - - - - - - - - -
- Hospitalized - - - - - - - - - - - - 1.00
- Recovered - - - - - - - - - - - - 1.00To retrieve the results, we use the run_multiple_get_results() function:
# Extracting the results
ans <- measles_model |>
run_multiple_get_results(
freader = data.table::fread
)
# Taking a look at the structure
str(ans)List of 2
$ outbreak_size :Classes 'epiworld_multiple_save_i', 'data.table' and 'data.frame': 10100 obs. of 5 variables:
..$ sim_num : int [1:10100] 1 1 1 1 1 1 1 1 1 1 ...
..$ date : int [1:10100] 0 1 2 3 4 5 6 7 8 9 ...
..$ virus_id : int [1:10100] 0 0 0 0 0 0 0 0 0 0 ...
..$ virus : chr [1:10100] "Measles" "Measles" "Measles" "Measles" ...
..$ outbreak_size: int [1:10100] 1 1 5 9 14 16 24 37 41 48 ...
..- attr(*, ".internal.selfref")=<externalptr>
..- attr(*, "what")= chr "outbreak_size"
$ hospitalizations:Classes 'epiworld_multiple_save_i', 'data.table' and 'data.frame': 5211 obs. of 6 variables:
..$ sim_num : int [1:5211] 1 1 1 1 1 1 1 1 1 1 ...
..$ date : int [1:5211] 11 16 19 20 21 22 23 24 25 26 ...
..$ virus_id: int [1:5211] 0 0 0 0 0 0 0 0 0 0 ...
..$ tool_id : int [1:5211] -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
..$ count : int [1:5211] 1 1 2 1 1 1 1 2 3 1 ...
..$ weight : int [1:5211] 1 1 2 1 1 1 1 2 3 1 ...
..- attr(*, ".internal.selfref")=<externalptr>
..- attr(*, "what")= chr "hospitalizations"
- attr(*, "class")= chr [1:2] "epiworld_multiple_save" "list"The function call will get us the results as a list of data.frames (data.table objects in this case). We will use the data.table package to manipulate the information.
# Converting into data.table format for convenience
library(data.table)
outbreak_size <- ans$outbreak_size |> as.data.table()
hospitalizations <- ans$hospitalizations |> as.data.table()Outbreak size
Finally, since we are only interested about the final outbreak size (in this case), can will collapse the data to get the total number of cases at the final simulation day. Subsequently, we can plot the results using the hist function:
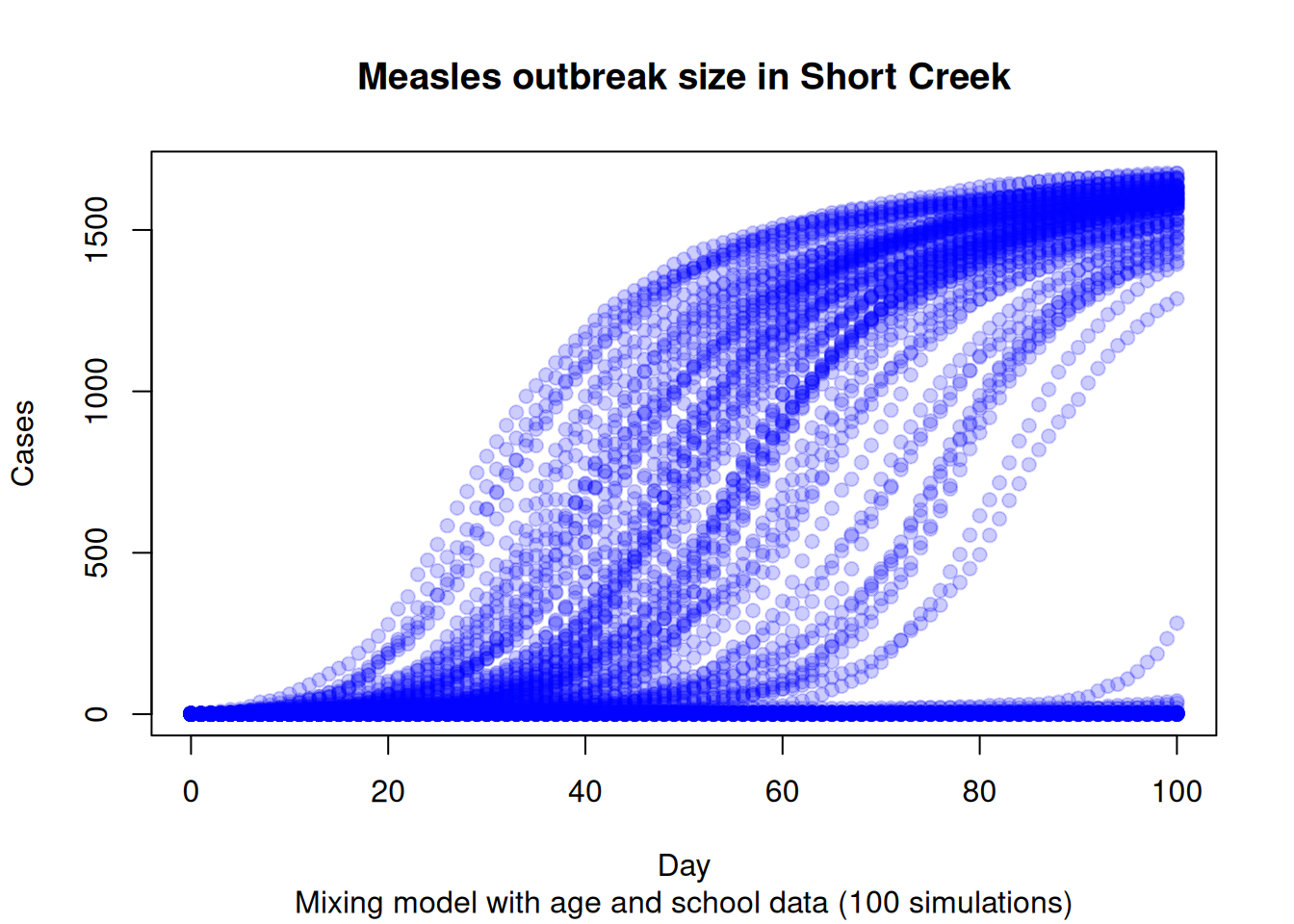
# Aggregating to get the final
with(
outbreak_size,
{
plot(
x = date,
y = outbreak_size,
col = adjustcolor("blue", alpha.f = .2),
pch = 19,
ylab = "Cases",
xlab = "Day",
main = "Measles outbreak size in Short Creek",
sub = "Mixing model with age and school data (100 simulations)"
)
})
We can also investigate the distribution of the final counts
Hospitalizations
In the case of the hospitalizations, we can draw a similar figure. The hospitalizations data contains the following information:
- Cases per virus (just measles in this case).
- Cases per tool (or the lack of). Information about “no tool” is recorded with a
tool_id == -1. - The counts (how many records in the data).
- Weights.
The weights attribute is to ensure that we take into consideration counting individuals more than once. For instance, if a model has more than one tool (not just vaccination), the individual who has two tools would be included twice in count. Thus, if we wanted to count the raw number of hospitalization cases, we would add across weight, but the count variable yields how many individuals were hospitalized under that combination of tool and virus id.
We can create a couple of boxplot to show how many cases we see per vaccination status:
hosp_tot <- merge(
hosp_tot[status == "Unvax", .(sim_num, unvax = total)],
hosp_tot[status == "Vax", .(sim_num, vax = total)],
all = TRUE
)
# Filling zeros
hosp_tot[, unvax := fcoalesce(unvax, 0L)]
hosp_tot[, vax := fcoalesce(vax, 0L)]
hosp_tot[, .(vax, unvax)] |>
as.matrix() |>
boxplot(
ylab = "Count",
xlab = "Status",
main = "Hospitalization per vaccination status",
sub = "Mixing model with age and school data (100 simulations)"
)
Final comments
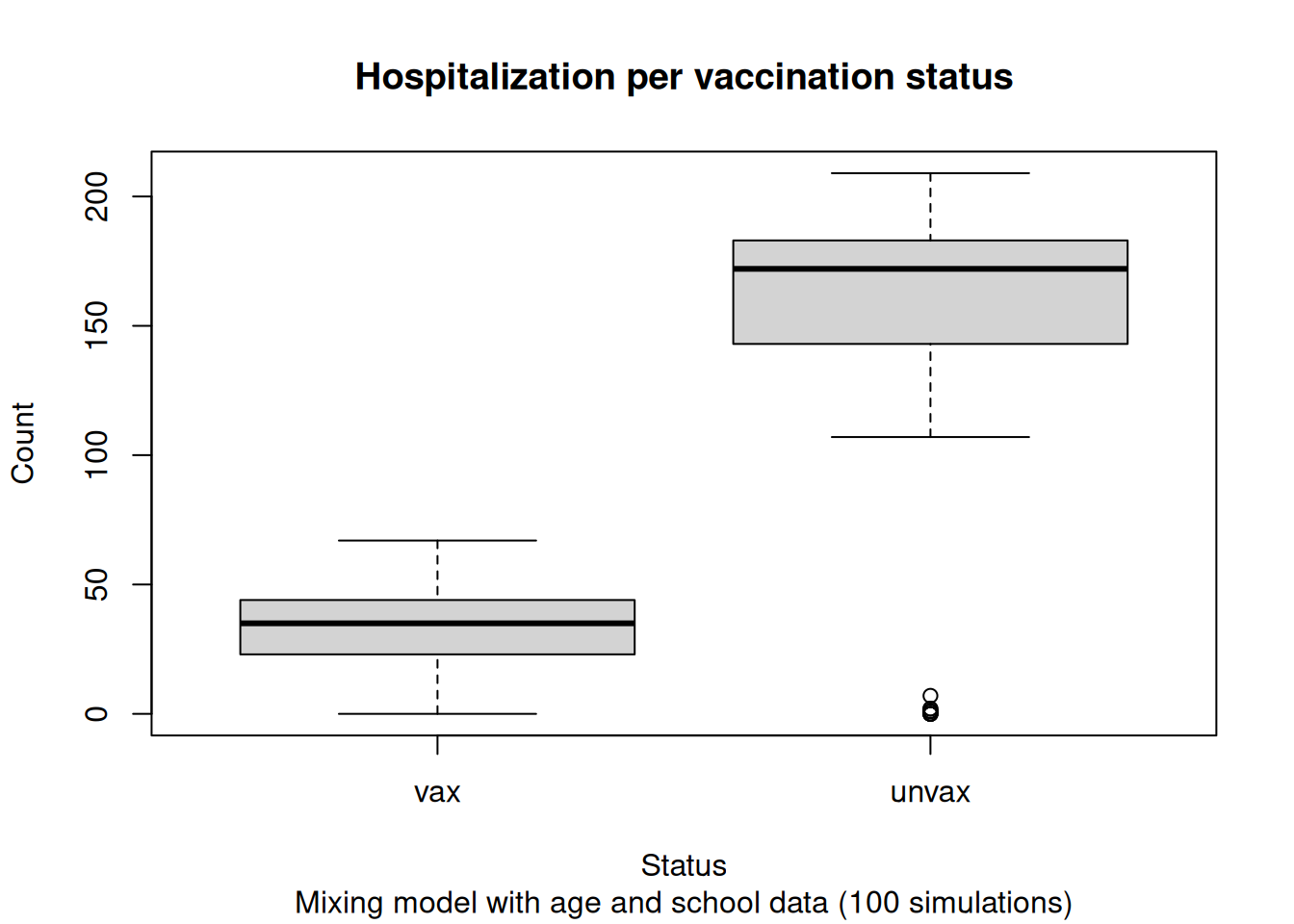
Ultimately, based on the current results, we would be expecting all unvaccinated individuals to become infected, with a small number of vaccinated individuals also getting infected. This is consistent with the high R0 of measles and the low vaccination rates in the area.