Part 2a: Non-Disease Applications - Network Diffusion
Though epiworldR focuses primarily on disease modeling, the epiworld framework is general enough to model any type of diffusion process, such as simulating the spread of ideas or rumors throughout a population. In this part of the workshop, we’ll walk through an example of social network diffusion.
Example Scenario: Academic Faculty Rumor
The example implements the following scenario:
- Rumor: The dean will resign!
- Population Description: A UK university faculty
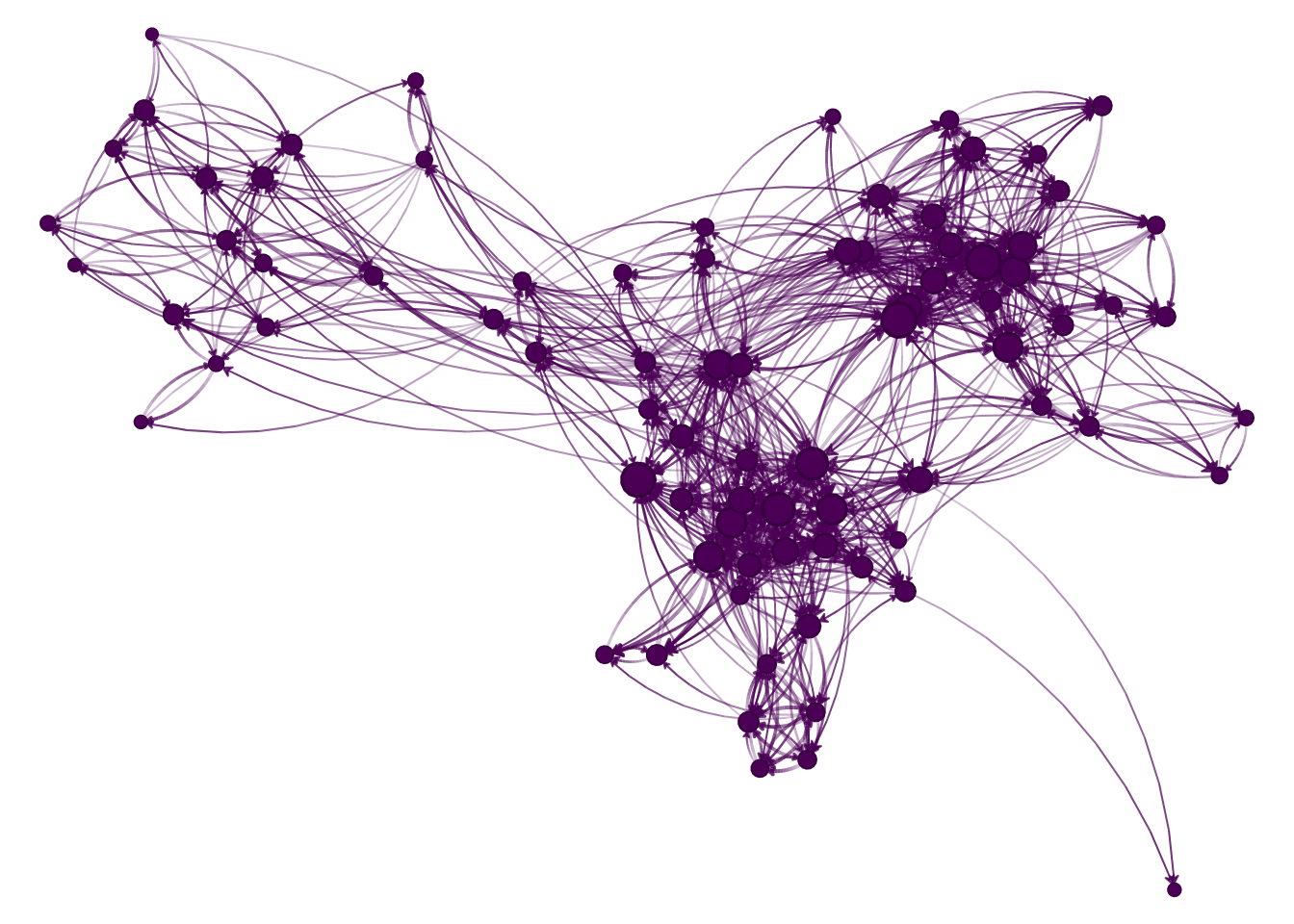
- Population size: 81 agents
- Initial rumor prevalence: 2 agents
- Probability of adopting the rumor: 0.1
Load Packages and Data
We use the igraph and netplot R packages for manipulating and plotting networks respectively. The file part2a.rda includes the UKfaculty friendship network from the igraphdata package, with the vertex attributes (UKfaculty_vertex) and edge list (UKfaculty_edgelist) as numeric matrices. We load the UKfaculty data and visualize the friendship network.
Simulating the Rumor
Using the ModelDiffNet() function, we can simulate how the rumor spreads through the network. First, we create the network diffusion model. The prevalence of the rumor is set such that 2 agents are exposed to the rumor at the start of the simulation. The probability of an agent adopting the rumor is 0.1.
We then initialize the model agents using the agents_from_edgelist() function.
We run the model for 100 days and plot the results.
________________________________________________________________________________
Diffusion of Innovations - The dean will resign!
It features 81 agents, 1 virus(es), and 0 tool(s).
The model has 2 states.
The final distribution is: 0 Non adopters, and 81 Adopters.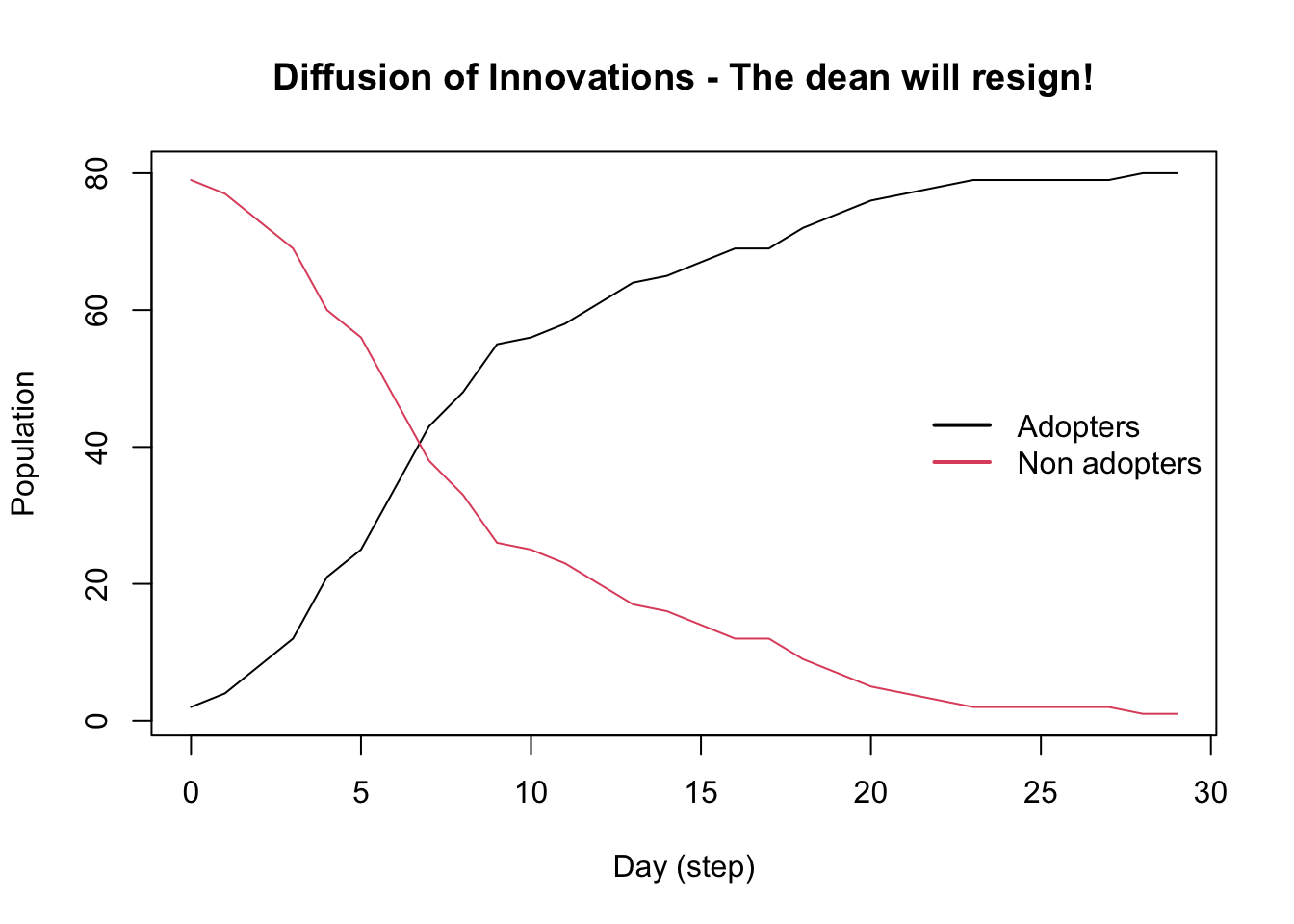
By day 16 or 17, the entire network had adopted the rumor that the dean will resign.
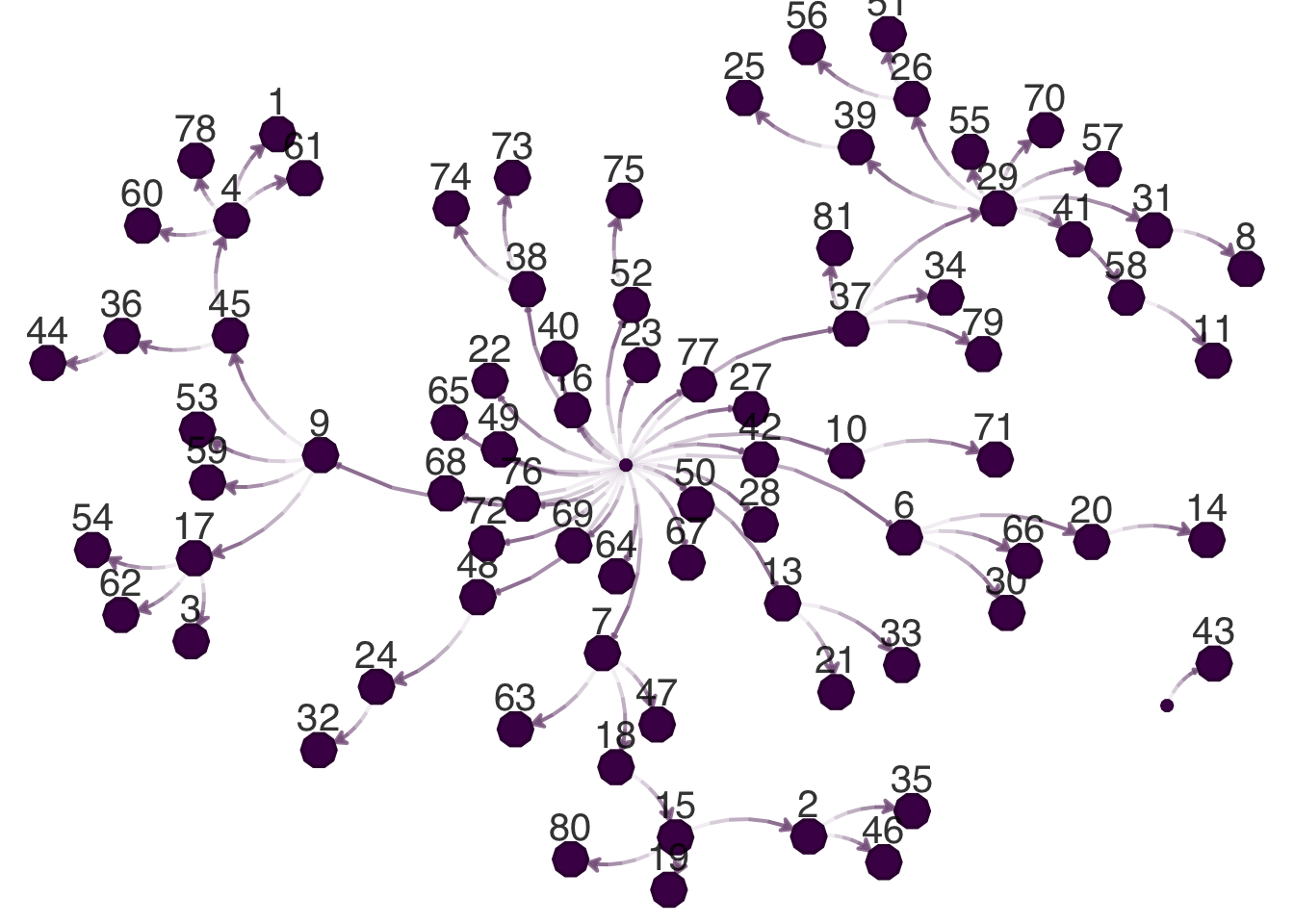
The transmission network is not always relevant for a diffusion network model, but in this case we can use it to visualize the spread of the rumor through the network. We get the transmission network using the get_transmissions() function, then plot the network using the igraph and netplot packages.
Warning in get_transmissions.epiworld_diffnet(adopt_rumor): The transmission
network is not necesarily relevant for the diffnet modelCode
Exercise
Create a diffusion network model using ModelDiffNet() to simulate the adoption of Chat-GPT among a population over 50 days.
- Population size: 10,000 agents
- Initial rumor prevalence: .01
- Probability of adopting ChatGPT: 0.1
-
Logit Params:
c(1, 4)
We’ve setup a synthetic network dataset for you to use.
Use the following parameters for agents_smallworld():
- n = 10000
- k = 8 (number of connections for each agent)
- d = FALSE (whether the graph is directed)
- p = .01 (probability of rewiring)
Create the model and run for 50 days, then plot the simulation with the plot() function.
Bonus Exercises and Exploration
If you want further exploration of network diffusion in epiworldR, here are some bonus topics and exercises to guide your learning.