Network Diffusion Model

The network diffusion model is a simple model that assumes that the probability of adoption of a behavior is proportional to the number of adopters in the network.

Usage

ModelDiffNet(
  name,
  prevalence,
  prob_adopt,
  normalize_exposure = TRUE,
  data = matrix(nrow = 0, ncol = 0),
  data_cols = 1L:ncol(data),
  params = vector("double")
)

# S3 method for class 'epiworld_diffnet'
plot(x, main = get_name(x), ...)

Arguments

name

Name of the model.

prevalence

Prevalence of the disease.

prob_adopt

Probability of adoption.

normalize_exposure

Normalize exposure.

data

Data.

data_cols

Data columns.

params

Parameters.

x

Object of class epiworld_diffnet.

main

Title of the plot

...

Passed to graphics::plot.

Value

An object of class epiworld_diffnet and epiworld_model.

Details

Different from common epidemiological models, the network diffusion model assumes that the probability of adoption of a behavior is proportional to the number of adopters in the network. The model is defined by the following equations: $$ P(adopt) = \mbox{Logit}^{-1}(prob\_adopt + params * data + exposure) $$ Where exposure is the number of adopters in the agent's network.

Another important difference is that the transmission network is not necesary useful since adoption in this model is not from a particular neighbor.

See also

Other Models: ModelSEIR(), ModelSEIRCONN(), ModelSEIRD(), ModelSEIRDCONN(), ModelSEIRMixing(), ModelSIR(), ModelSIRCONN(), ModelSIRD(), ModelSIRDCONN(), ModelSIRLogit(), ModelSIRMixing(), ModelSIS(), ModelSISD(), ModelSURV(), epiworld-data

Examples

set.seed(2223)
n <- 10000

# Generating synthetic data on a matrix with 2 columns.
X <- cbind(
  age = sample(1:100, n, replace = TRUE),
  female = sample.int(2, n, replace = TRUE) - 1
)

adopt_chatgpt <- ModelDiffNet(
  "ChatGPT",
  prevalence = .01,
  prob_adopt = .1,
  data       = X,
  params     = c(1, 4)
)

# Simulating a population from smallworld
agents_smallworld(adopt_chatgpt, n, 8, FALSE, .01)

# Running the model for 50 steps
run(adopt_chatgpt, 50)
#> _________________________________________________________________________
#> |Running the model...
#> |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| done.
#> | done.

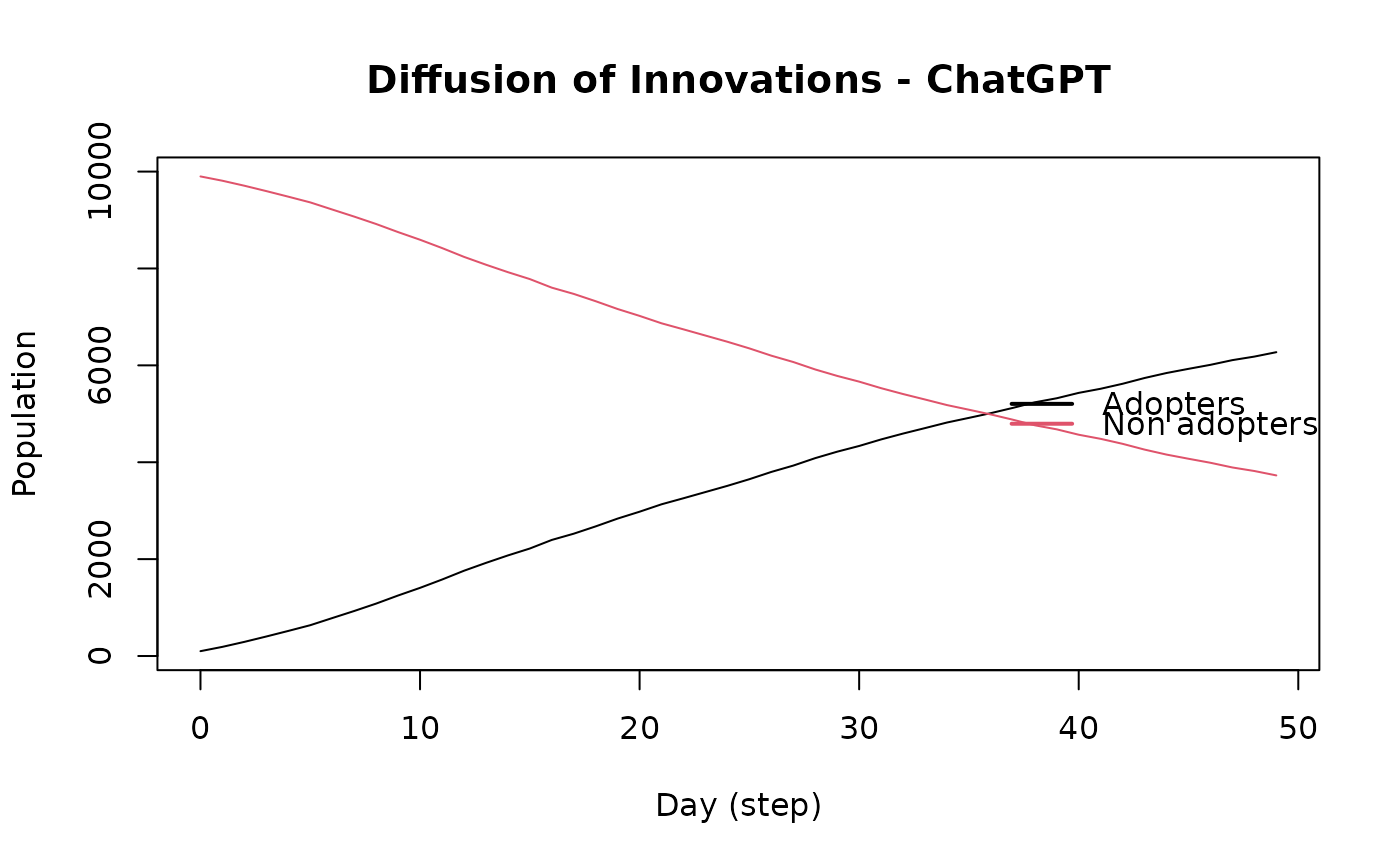
# Plotting the model
plot(adopt_chatgpt)